Jmarti传输线→相域频率相关线参数转换
- 文档
- 2025-04-16
- 30热度
- 3评论
Jmarti模型→相域模型参数转换
- Jmarti模型说明
参考《J. Marti, “Accurate Modelling of Frequency-Dependent Transmission Lines in Electromagnetic Transient Simulations,” IEEE Trans. Power Appar. Syst., vol. PAS-101, no. 1, pp. 147–157, Jan. 1982, doi: 10.1109/TPAS.1982.317332.》文献,Jmarti模型建模方法如下:

其中,两侧阻抗表示如下,其中ko,ki,pi参数会在adpss等软件中提供:
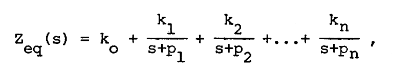
在Jmarti模型中,阻抗网络会被建模成RC并联回路串联的形式。
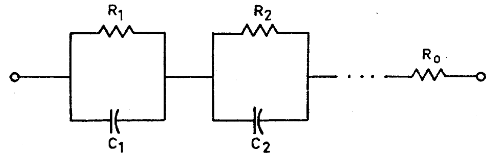
其中:
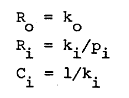
对于注入电流源方面,Jmarti本质上是构建了电压的传递关系,将用Forward和Backward表示。
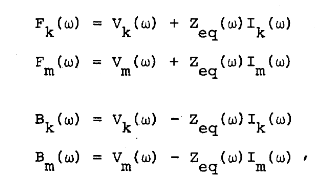
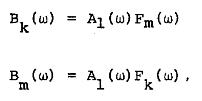
最终,电压表示为:
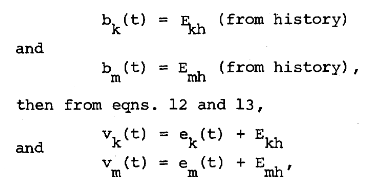
此外,值得一提的是ADPSS中,Jmarti模型是以模态形式呈现的,且相模转换矩阵是常数矩阵。也就是说,对于3个导体的传输线,Jmarti模型的Zeq和传递函数A都可以看作是模域下的3维的对角阵。
而相域模型没有这样的要求,输入参数可以是3*3的相域矩阵。
- 戴维南等值→诺顿等值的转换
Jmarti模型每一侧可表述为戴维南等值模型:
\[
\begin{align}
& V_{k}^{hist}(t)=\int_{0}^{t-\tau }{\left[ {{v}_{m}}(u)+{{Z}_{eq}}{{i}_{m}}(u) \right]}{{a}_{1}}(t-u)du \\
& {{Z}_{eq}}(s)={{k}_{0}}+\sum\limits_{i=1}^{n}{\frac{{{k}_{i}}}{s+{{p}_{i}}}} \\
\end{align}
\]
其中a1为电压电流信号传输矩阵,这里是卷积计算。
戴维南等值模型和诺顿等值模型应完全等价
\[\begin{align}
& I_{k}^{hist}(t)=\frac{1}{{{Z}_{eq}}}\int_{0}^{t-\tau }{\left[ {{v}_{m}}(u)+{{Z}_{eq}}{{i}_{m}}(u) \right]}{{a}_{1}}(t-u)du \\
& =\int_{0}^{t-\tau }{\left[ \frac{{{v}_{m}}(u)}{{{Z}_{eq}}}+{{i}_{m}}(u) \right]}{{a}_{1}}(t-u)du \\
& {{G}_{eq}}={{Z}_{eq}}^{-1}
\end{align}\]
从频域上来说,电流的式子应该写成
\[
\begin{align}
& I_{k}^{hist}(s)=\frac{1}{{{Z}_{eq}}\left( s \right)}\left[ {{v}_{m}}(s)+{{Z}_{eq}}\left( s \right){{i}_{m}}(s) \right]{{a}_{1}}\left( s \right) \\
& =\left[ \frac{{{v}_{m}}(s)}{{{Z}_{eq}}\left( s \right)}+{{i}_{m}}(s) \right]{{a}_{1}}\left( s \right) \\
& =\left[ {{i}_{m}}(s)+{{G}_{eq}}\left( s \right){{v}_{m}}(s) \right]{{a}_{1}}\left( s \right)
\end{align}
\]
即:
\[
I_{k}^{hist}(t)=\int_{0}^{t-\tau }{\left[ {{G}_{eq}}{{v}_{m}}(u)+{{i}_{m}}(u) \right]}{{a}_{1}}(t-u)du
\]
可以注意到传输矩阵无需转换,可以复用。
- Zeq→Geq的转换
我们这里先考虑一相的场景。
如何将[math]{{Z}_{eq}}(s)={{k}_{0}}+\sum\limits_{i=1}^{n}{\frac{{{k}_{i}}}{s-{{p}_{i}}}}[/math]转换成[math]{{G}_{eq}}(s)={{g}_{0}}+\sum\limits_{i=1}^{n}{\frac{{{g}_{i}}}{s-{{q}_{i}}}}[/math]是关键问题,本质上就是求Zeq的零点。可以将Zeq(s)写成传递函数矩阵形式:
\[
sX\left( s \right)=PX\left( s \right)+Ku\left( s \right)
\]
\[
y\left( s \right)=CX\left( s \right)+{{k}_{0}}u\left( s \right)
\]
\[
P=\left[ \begin{matrix}
{{p}_{1}} & {} & {} \\
{} & {{p}_{i}} & {} \\
{} & {} & {{p}_{n}} \\
\end{matrix} \right]
\]
\[
K=\left[ \begin{align}
& {{k}_{1}} \\
& {{k}_{i}} \\
& {{k}_{n}} \\
\end{align} \right]
\]
\[
C=\left[ \begin{matrix}
1 & \cdots & 1 \\
\end{matrix} \right]
\]
\[
y\left( s \right)=\left[ C{{\left( s\mathbf{I}-\mathbf{P} \right)}^{-1}}K+{{k}_{0}} \right]u\left( s \right)
\]
对应的,写出Geq的传递函数矩阵(输入y(s),输出u(s))
\[
\begin{align}
& sX\left( s \right)=\left( P-\frac{KC}{{{k}_{0}}} \right)X\left( s \right)+\frac{1}{{{k}_{0}}}y\left( s \right) \\
& u\left( s \right)=-\frac{C}{{{k}_{0}}}X\left( s \right)+\frac{1}{{{k}_{0}}}y\left( s \right) \\
& u\left( s \right)=\left[ \frac{1}{{{k}_{0}}}-\frac{C}{{{k}_{0}}^{2}}{{\left( s\mathbf{I}-P+\frac{KC}{{{k}_{0}}} \right)}^{-1}} \right]y\left( s \right) \\
\end{align}
\]
现在要求这个传递函数矩阵的极点,也就是矩阵[math]\left( P-\frac{KC}{{{k}_{0}}} \right)[/math]的特征值即可。可调用python的np.linalg.eigvals库函数来求解。
\[
Q=eig\left( P-\frac{KC}{{{k}_{0}}} \right)
\]
下一步就是计算留数gi了,这里采用留数定理:
\[
{{g}_{i}}=\underset{s\to {{q}_{i}}}{\mathop{\lim }}\,\left( s-{{q}_{i}} \right){{G}_{eq}}\left( s \right)=\underset{s\to {{q}_{i}}}{\mathop{\lim }}\,\frac{\left( s-{{q}_{i}} \right)}{\frac{\prod\nolimits_{1}^{n}{\left( s-{{q}_{i}} \right)}}{\prod\nolimits_{1}^{n}{\left( s-{{p}_{i}} \right)}}}=\frac{\prod\nolimits_{1}^{n}{\left( {{q}_{i}}-{{p}_{i}} \right)}}{\prod\nolimits_{j\ne i}{\left( {{q}_{i}}-{{q}_{j}} \right)}}
\]
- 模态→相域转换
以上都是在单相条件下推导,不过对于Jmarti模型,都是考虑各个模态独立的,以直流模型(2个导体)为例,ADPSS中的Jmarti模型参数定义如下:
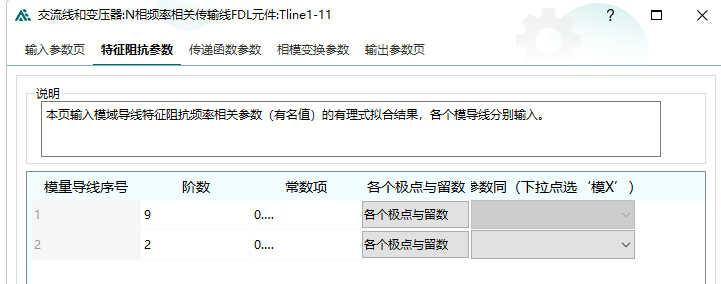
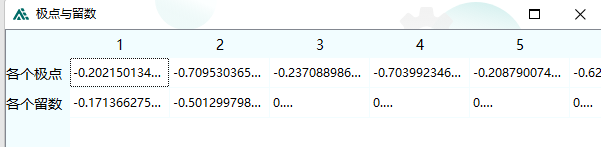
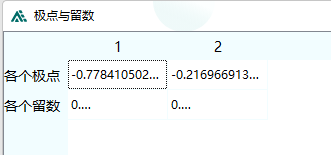
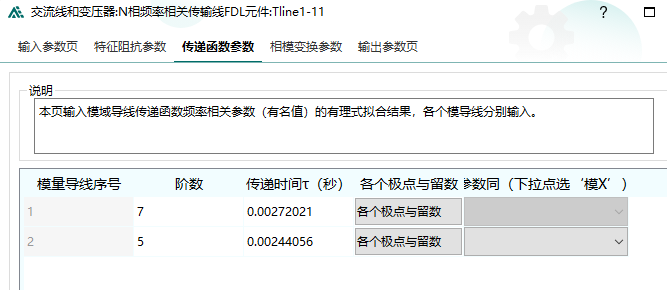
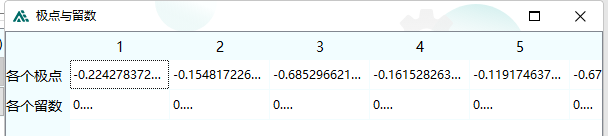
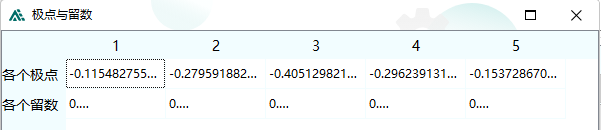
ADPSS中还要求输入相模变换矩阵。
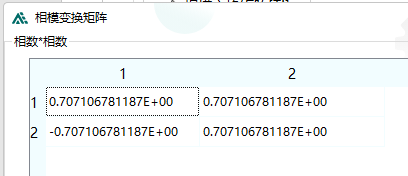
注意到给的阻抗和传输矩阵的数据都是2维的,每一维分别给一些极点和留数,所以可认为其模态阻抗和传输矩阵就是对角阵,可直接通过相模变换矩阵反变换到相域下。
- 测试
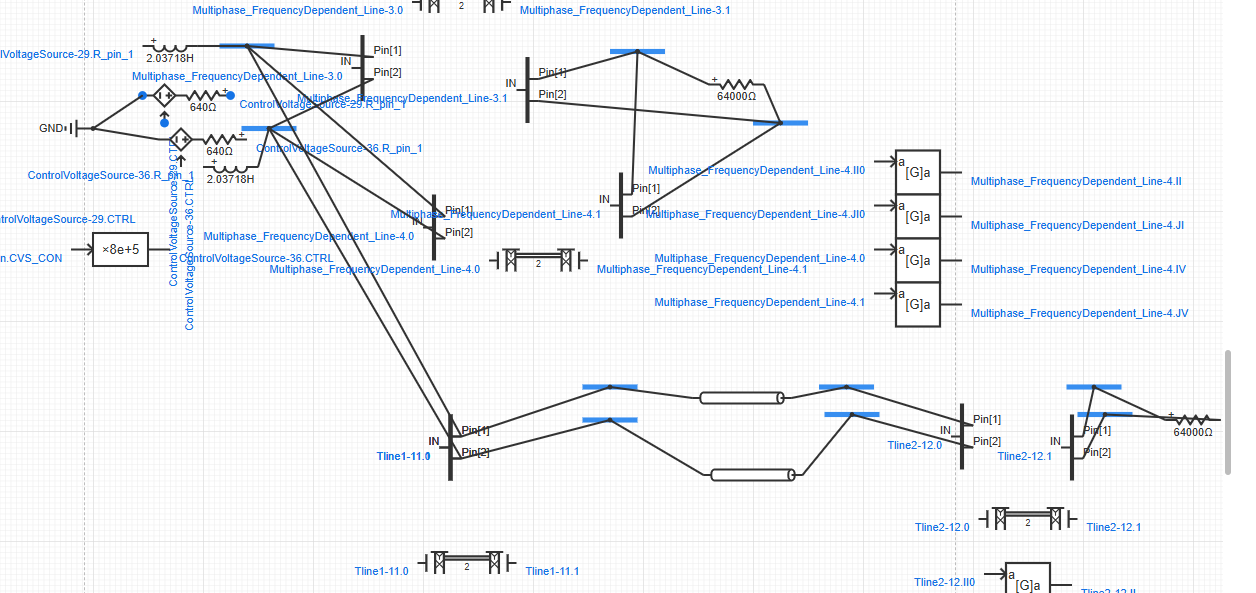
构建了送端±800kV,受端接10pu电阻的测试算例。正极叠加1Hz,160kV的电压跌落,负极叠加2Hz,80kV的正弦电压。
输出部分对比结果
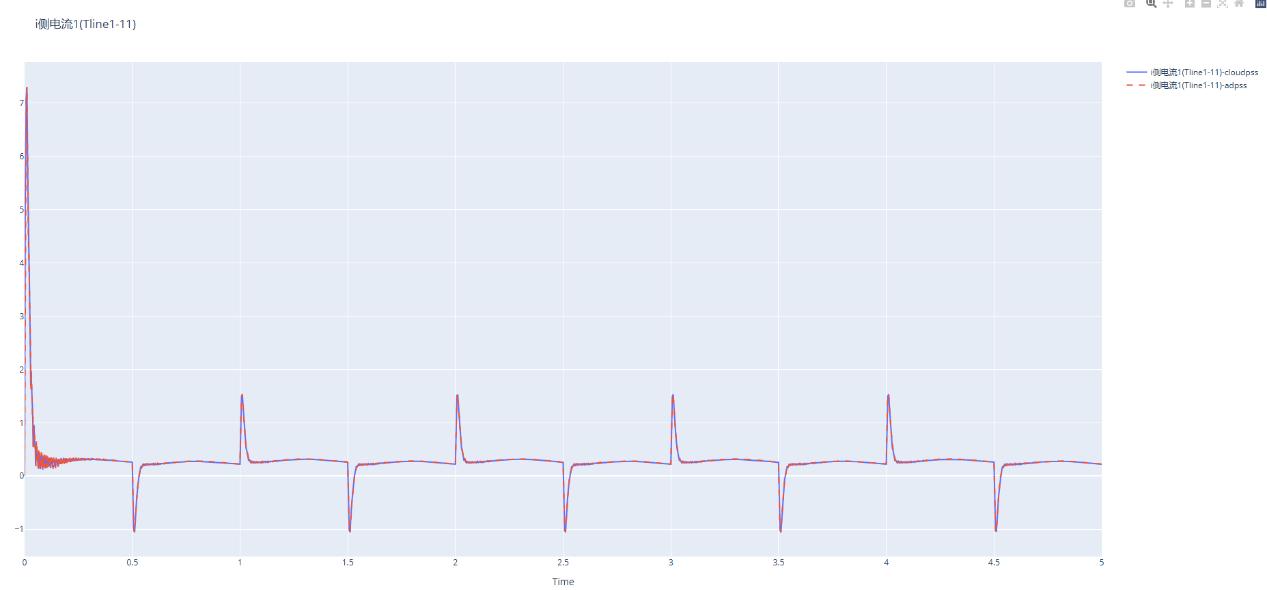
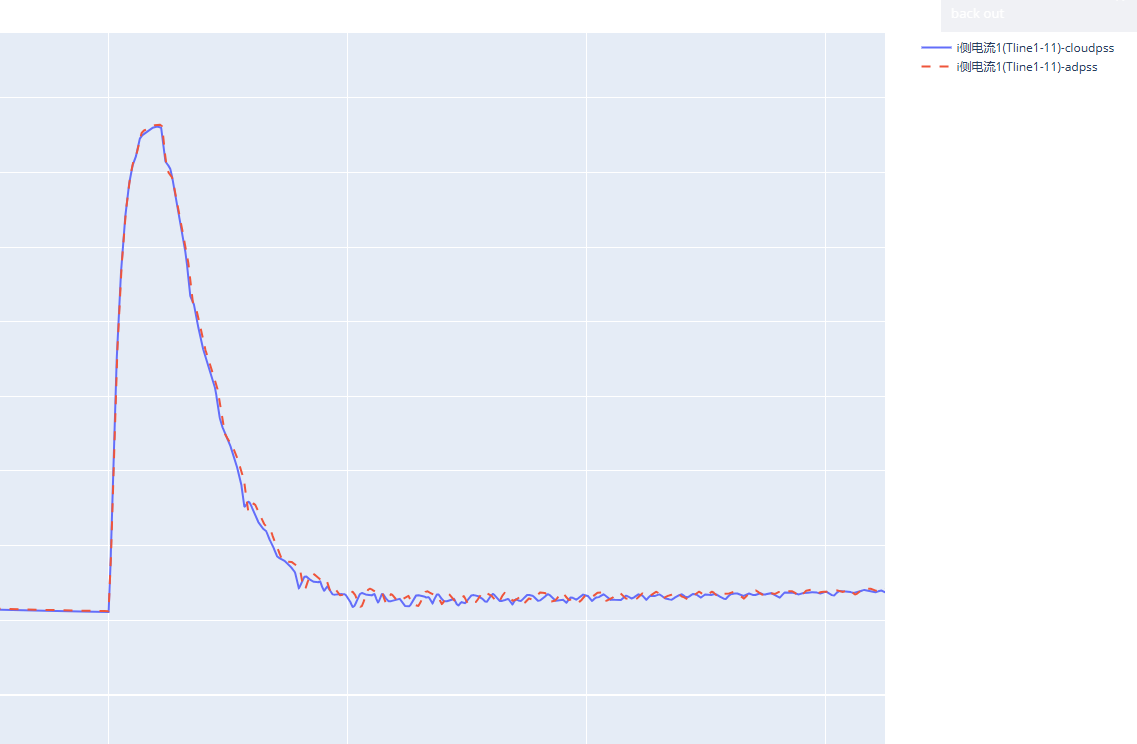
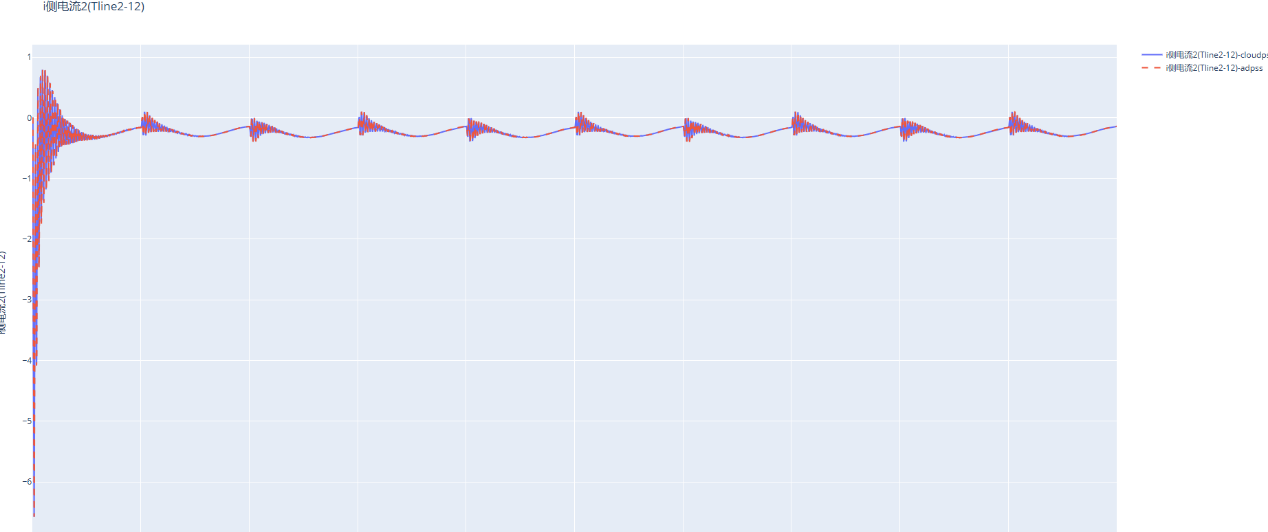
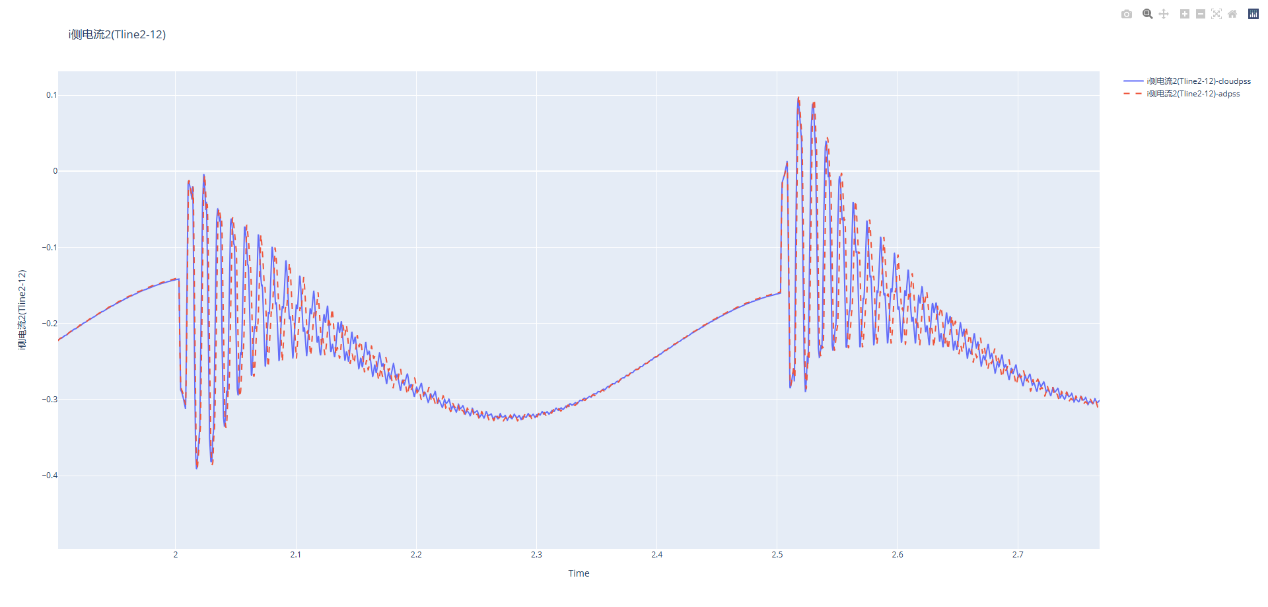
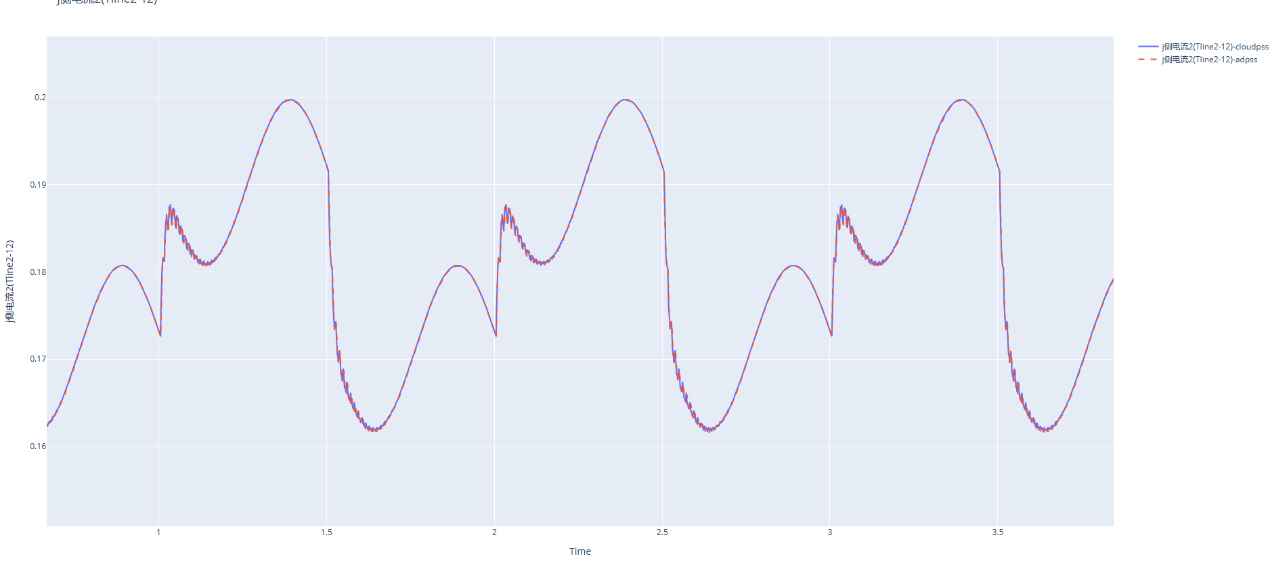

人生多艰,快乐一天是一天!
时间真快,一年又快结束了,啥也不说了,祝你幸福吧!